Some basic operations of set theory, and corresponding tools for representation, can simplify counting and probability computations. The operations to which we refer here are intersection, union, and complement.
If we have an ambient set $S\,$ , with subsets $A$ and $B$ (in terms of notation: $\, A\,$ , $\, B\subset S\,$ ), then
$A\cap B =$ the collection of elements of $S$ in both $A$ and $B\,$ ,
$A\cup B =$ the collection of elements of $S$ in at least one of $A$ or $B\,$ , and
$A\setminus B =$ the collection of elements of $S$ in $A$ but not in $B\;$ .
Examples of Subsets Constructed Using Set Operations
Throughout the following, we will use $A\,$ , $\, B\,$ , and $C$ to denote subsets of an ambient set $S\;$ . Various constraints or allowances on subsets of an ambient set $S$ are conveniently expressed using set operations. These make for shortcuts in counting and probability computations. Here are some examples.
- We can see immediately that $A\setminus B =A\cap B^c\,$ , as $x\in A\setminus B$ means that $x\in A$ and that $x\not\in B\;$ . Thus $x\in A$ and $x\in B^c\;$ .
- We can also see that $A\cap (B\cup C) =(A\cap B)\cup (A\cap C)\;$ . This is because $x\in A\cap (B\cup C)$ means that $x\in A$ and $x\in$ at least one of $B$ or $C\;$ . If $x\in B$ then $x\in A\cap B$ and hence in $(A\cap B)\cup (A\cap C)\;$ . Similarly if $x\in C$ then $x\in A\cap C$ and hence in $(A\cap B)\cup (A\cap C)\;$ . This shows that anything in $A\cap (B\cup C)$ is in $(A\cap B)\cup (A\cap C)\;$ . To see that nothing of $(A\cap B)\cup (A\cap C)$ is missed, suppose that we have some $x\in (A\cap B)\cup (A\cap C)\;$ . Then $x\in$ at least one of $A\cap B$ or $A\cap C\;$ . Suppose $x\in A\cap B\;$ . Then $x\in A\,$ , and $x\in B$ hence $x\in B\cup C\;$ . It follows that $x\in A\cap (B\cup C)\;$ . Similarly, if $x\in A\cap C$ then $x\in A\cap (B\cup C)\;$ . Thus the two sets $A\cap (B\cup C)$ and $(A\cap B)\cup (A\cap C)$ have the exact same elements and are thus equal.
- It can be seen in a similar fashion that $A\cup (B\cap C) =(A\cup B)\cap (A\cup C)\;$ . Reasoning to verify this is left to the reader.
- More complicated is an understanding of the “exclusive or”: $\, (A\cup B) \setminus (A\cap B)\;$ . Reading this, we see that it is the collection of elements of at least one of $A$ or $B$ ( $\, A\cup B\,$ ), but not both (as $A\cap B$ is removed. Thus it is the collection of elements which are in exactly one of $A$ or $B\;$ . Since $\displaystyle{ A\cap B^c }$ is the collection of elements of only $A\,$ , and $\displaystyle{ B\cap A^c }$ is the collection of elements of only $B\,$ , $\displaystyle{ \left( A\cap B^c\right) \cup \left( B\cap A^c\right) }$ is the collection of elements which are in exactly one of $A$ or $B\;$ . Thus $\displaystyle{ (A\cup B) \setminus (A\cap B) = \left( A\cap B^c\right) \cup \left( B\cap A^c\right) }\;$ .
This “exclusive or” might occur when determining betting odds while playing poker. It is typical to consider straight flushes, i.e. hands which are simultaneously straights and flushes, as a special betting category. Thus the five card hand $7\diamondsuit\,$ , $\, 8\diamondsuit\,$ , $\, 9\diamondsuit\,$ , $\, 10\diamondsuit\,$ , $\, J\diamondsuit$ would be a straight flush. These hands comprise the intersection of the collections of straights and flushes. When computing the number of ways a straight can occur, or the number of ways a flush can occur, it is common to omit this intersection as it is a separate betting category.
Restaurants also typically use the “exclusive or” when offering a choice: one ordering a steak one can get a cup of soup or a salad, but not both. Thus it is that the exclusive or tends to be how we typically use the word “or” in common parlance.
Properties of Set Operations
Here are several convenient properties of set operations for future reference:
- $A\cup B =B\cup A$
- $A\cap B =B\cap A$
- $A\cup (B\cap C) =(A\cup B)\cap (A\cup C)$ (already seen above)
- $A\cap (B\cup C) =(A\cap B)\cup (A\cap C)$ (also already seen above)
- $A\cup (B\cup C) =(A\cup B)\cup C$ (usually written $A\cup B\cup C\,$ )
- $A\cap (B\cap C) =(A\cap B)\cap C$ (usually written $A\cap B\cap C\,$ )
- $\displaystyle{ (A\cup B)^c =\left( A^c\cap B^c\right) }$
- $\displaystyle{ (A\cap B)^c =\left( A^c\cup B^c\right) }$
Here is a nice example of how one might use set operations to count, and so determine an otherwise complicated probability.
Example: Among thirty people, what is the probability that some pair will share a birthday?
A slight simplification: we will assume that none of the thirty people is born on 29 Feb. We will also number the thirty people #1, #2, … , #30. As there are $365$ dates possible for the birthday of each of the people, the number of possible ways to have birthdays among the people is $365^{30}\;$ . This is a huge number which is unreasonable to try to write down in other than exponential format. Let $S$ denote the set of possible assignments of birthdays.
Let $A\subset S$ denote the set of birthday assignments for which there is no pair sharing birthdays. Then $A^c\subset S$ is the set of birthday assignments for which there is at least one pair of people sharing a birthday. The reason for this distinction is that it is easy to determine the size of $A$ and then subtract this from the size of $S$ to get the size of $A^c\;$ . The reader is invited to consider how one might try to determine the number of elements of $A^c$ directly – and it is suggested that one proceed by examining a very simple case, like five people and ten possible days.
We now proceed to determine the size of $A\;$ . There are $365$ possible birthdays for person #1. If person #2 does not have the same birthday as person #1, then there are $364$ possible birthdays for #2. Continuing, we see that there are $363$ possible birthdays for #3, $\,362$ possible birthdays for #4, … , $\,336$ possible birthdays for #30. The number of ways to have thirty people with mutually distinct birthdays is thus
$$ \#(A) =365\times 364 \times \cdots \times 336 =\frac{365!}{335!} =P^{365}_{30} \;\text{.} $$
This makes sense, as we are ordering $30$ of the $365$ days in the year.
Thus the number of elements of $S$ for which there is some matching pair is
$$ \#(A^c) =365^{30} -\frac{365!}{335!} \;\text{.} $$
We can compute that the probability of no two people sharing a birthday is
$$ P(A) =\frac{\#(A)}{365^{30}} \doteq 0.2937 $$
and the probability that some pair shares a birthday is
$$ P(A^c) =\frac{\#(A^c)}{365^{30}} \doteq 0.7063 \;\text{.} $$
The fact is that in a room with at least $23$ people, the probability is greater than $0.5$ that some pair will share a birthday. Try this as a playful bet at a gathering. Bet on the pair. One has a better chance to win than lose.
It is often useful to have visualizations tools when dealing with abstract concepts. Such a tool is available here in the notion of Venn diagrams.
Venn Diagrams
A particularly useful way to visualize the relationship between sets is available with Venn diagrams. These are diagrams representing a universal set $S$ by a region (usually rectangular), and subsets (denoted by $A$ , $\, B\,$ , etc.) of $S$ by regions within the rectangle (often circular).
Shown below is a Venn diagram with three subsets (denoted by $A$ , $\, B\,$ , and $C\,$) of a universal set $S\;$ . A list of some of the possible subsets of $S$ formed by intersections and unions of $A$ , $\, B\,$ , and $C$ is available in the attached drop-down menu, and the particular subset will be highlighted when selected. (This is currently not functional – the image is the Venn diagram of three generic sets.)
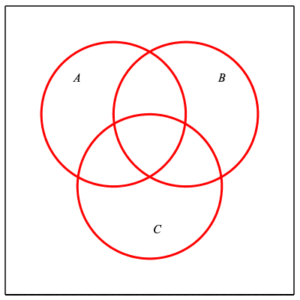
One use of Venn diagrams is to help keep track of subsets of $S\;$ . Consider the following examples.
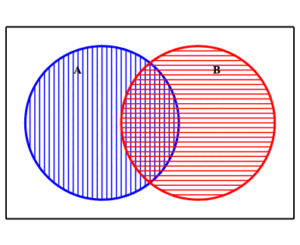
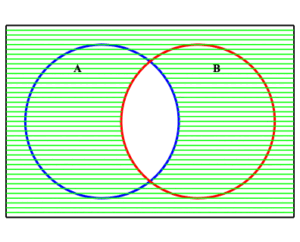
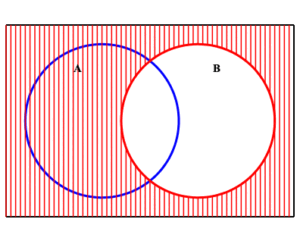
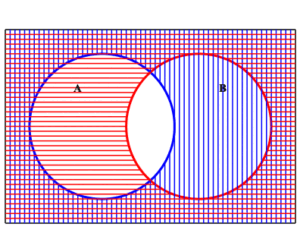
Example: Venn diagram illustrating $\displaystyle{ (A\cap B)^c =\left( A^c\cup B^c\right) }$
Illustrated here are the sets $A\cap B$ and its complement $\displaystyle{ (A\cap B)^c }\;$ .
|
|
| $A$ in blue, $\,B$ in red, $\, A\cap B$ is overlap | $\displaystyle{ (A\cap B)^c }$ in green |
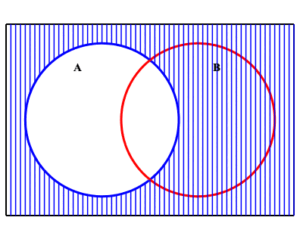
We see that this complement is the union of the two sets $\displaystyle{ A^c }$ and $\displaystyle{ B^c }\;$ .
|
|
| complement of $A$ | complement of $B$ |
|
|
| $A^c \cup B^c$ | |
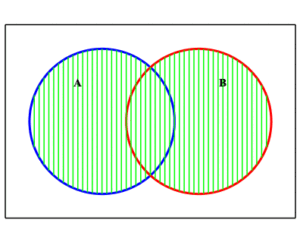
Example: Venn diagram illustrating
$\displaystyle{ (A\cup B) \setminus (A\cap B) = \left( A\cap B^c\right) \cup \left( B\cap A^c\right) }$
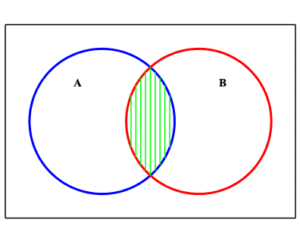
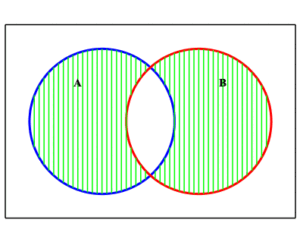
Illustrated here are the set $A\cup B$ and $A\cap B\,$ , along with their difference $(A\cup B) \setminus (A\cap B)\; $ .
|
|
|
| $A\cup B$ | $A\cap B$ | $(A\cup B)\setminus (A\cap B)$ |
We see that this is the union of the two shaded sets $\displaystyle{ A\cap B^c }$ and $\displaystyle{ B\cap A^c }\;$ .
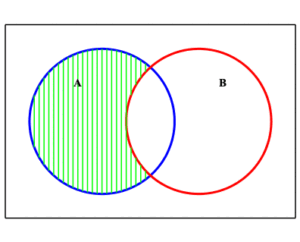
|
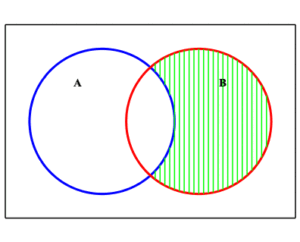
|
| $A\cap B^c$ | $B\cap A^c$ |

