Perhaps the easiest probabilities to determine are when there are a finite number of possible outcomes to an experiment, and each outcome is equally likely. In this case the probability of an event is the number of outcomes that make up the event divided by the total number of outcomes. Thus, for example, on the experiment of rolling a fair
six-sided die there are exactly six possible outcomes: $1\,$ , $\, 2\,$ , $\, 3\,$ , $\, 4\,$ , $\, 5$ and $6\;$ . There are exactly two ways to get an outcome greater than $4$ (i.e. $\, 5$ and $6\,$ ), so the probability of the event “a roll of the die is greater than $4\,$ ” is
$$\frac{\text{number of outcomes greater than } \,4}{\text{number of possible outcomes}} =\frac{2}{6} =\frac{1}{3}\; .$$
Another easy example is the probability of being dealt a face-card ( $J\,$ , $\, Q$ or $K\,$ ) from a fair deck. Since there are fifty-two cards in a deck, and twelve of them are face-cards ( $J\clubsuit\,$ , $\, J\diamondsuit\,$ , $\, J\heartsuit\,$ , $\, J\spadesuit\,$ , $\, Q\clubsuit\,$ , $\, Q\diamondsuit\,$ , $\, Q\heartsuit\,$ ,
$\, Q\spadesuit\,$ , $\, K\clubsuit\,$ , $\, K\diamondsuit\,$ , $\, K\heartsuit\,$ , $\, K\spadesuit\,$ ), the probability of being dealt a face-card is
$$\frac{\text{number of face-cards}}{\text{number of possible cards}} =\frac{12}{52} =\frac{3}{13}\; .$$
The biggest difficulty here is that all too often it is not obvious how to count all of the possible outcomes for an experiment, or the number of outcomes comprising an event. For example, suppose we are dealt a five-card hand from a fair deck. What is the probability that the five cards make up a full house (three cards of one value and two of another)? Answering this requires two counts: the number of possible five-card hands and the number that are full houses. These are less obvious than the counts mentioned above.
We will address the above counts shortly. But for our purposes it will help to have a few techniques available. In developing these techniques we will analyze easier examples and build up enough know-how to address the above problem.
Counting Multistep Processes
• Two-Step Processes
If a process has two steps, where there are three outcomes for the first step and (no matter how the first step played out) two for the second, then there are six possible outcomes for this two-step process. Thus if we have three balls ( A, B, and C) and a participant is to pick first one of them and then another, no matter which of the three possible choices the participant makes for the first pick there are two choices for the second. Denoting by AB the event where the participant first picks ball A and then ball B, and similarly for other choices, here are the possible outcomes of the experiment: AB, AC, BA, BC, CA, CB.
This understanding works when the number of possible outcomes is substantially greater in each of the steps of a two-step process. If the first step has $\displaystyle{ n_1 }$ possible outcomes, and the second has $\displaystyle{ n_2 }$ possible outcomes, the two-step process has $\displaystyle{ n_1\cdot n_2 }$ possible outcomes.
We can see this, for example, in the process of choosing first a hospital and then a doctor, given that there are eight hospitals and each has fifty doctors. The analysis above indicated that there would be $8\cdot 50 =400$ possible outcomes for this process. In a similar fashion, we can determine the number of ways to be dealt two cards in order from a fair fifty-two card deck. There are fifty-two possible first cards and, for each of these, there are fifty-one possible second cards. Thus the number of outcomes of this process is $52\cdot 51=2652\;$ .
It would be a bit onerous to list – at least by hand – all of the possible outcomes for the two-card experiment just mentioned. A more easily displayed problem/solution is the number of ways to receive two items in order from a collection of six items labelled $A\,$ , $\, B\,$ , $\, C\,$ , $\, D\,$ , $\, E\,$ , and $F\;$ . We know from the above discussion that the number of possible outcomes for this process is $6\cdot 5 =30\;$ . Attempt to list the thirty possible ways to receive first one of the six items and then one of the remaining five. A solution is given below.
Solution
$$
\begin{array}{rcccccc}
\text{first choice:} & A & B & C & D & E & F \\ \hline
& AB & BA & CA & DA & EA & FA \\ & AC & BC & CB & DB & EB & FB \\
\text{possibilities:} & AD & BD & CD & DC & EC & FC \\ & AE & BE & CE & DE & ED & FD \\
& AF & BF & CF & DF & EF & FE
\end{array}
$$
• Many-Step Processes
When confronted with a three-step, or four-step, or more-step, process, a useful trick is to consider it as a two-step process as follows. This is described in the case of a three-step process, though it extends to processes requiring any finite number of steps. Examples with more than three steps will be given.
Consider for now an extension of the process described at the end of the discussion of two-step processes. That is, we wish now to determine the number of ways to receive three items in order from the collection of six items labelled $A\,$ , $\, B\,$ , $\, C\,$ , $\, D\,$ , $\, E\,$ , and $F\;$ .
We will do this by considering the new three-step process as a two-step process where the first step is receiving two items from the collection – i.e. precisely the process already treated – and the second step of this new point of view is receiving the third item from the remaining items after the first two have been received. As shown, there are thirty outcomes for the first step of this two-step process. Then, no matter the initial step, there are four possible second steps (receiving the third item). Thus for this process there are $30\cdot 4 =120$ possible outcomes.
In general, given a three-step process where there are $\displaystyle{ n_1 }$ possible outcomes for the first step, $\,\displaystyle{ n_2 }$ possible outcomes for the second step, and $\displaystyle{ n_3 }$ possible outcomes for the third step, we will consider this process as a two-step process as follows. Consider the first two steps of our process as a single step from our new point-of-view. There are $\displaystyle{ n_1\cdot n_2 }$ possible outcomes for this first step. Now the second step from our new point-of-view is the third step under our original three-step point of view. Thus there are still $\displaystyle{ n_3 }$ possible outcomes for this step. For the new point-of-view two-step process there are thus $\displaystyle{ \left( n_1\cdot n_2 \right) \cdot n_3 = n_1\cdot n_2\cdot n_3 }$ possible outcomes.
We see this, for example, on considering the three-step process of first choosing a hospital, then a doctor, then a treatment plan, given that there are eight hospitals, each has fifty doctors, and each doctor has a choice of four treatments. With respect to our new two-step point-of-view, we will consider first choosing a hospital then a doctor as one step, and we have seen that there are $400$ possible outcomes for this step. The second step will be the choice of treatment, so that there are $400\cdot 4 =1600 \; (=8\cdot 50\cdot 4)$ possible outcomes for this process.
More generally, for a $k\,$-step process where there are $\displaystyle{ n_1 }$ possible outcomes for the first step, $\,\displaystyle{ n_2 }$ possible outcomes for the second step, etc. up to $\displaystyle{ n_k }$ possible outcomes for the $k$-th step, there are $\displaystyle{ n_1\cdot n_2\cdot \dots \cdot n_k }$ possible outcomes for the entire process. We can build up this computation by adding one step at a time, and with each new step consider the preceding computation as a single step and the newly added step as the second step of a two-step process.
As an example, note that if we are dealt five cards in order from a fair deck, there are $52$ possible outcomes for the first card, $\, 51$ for the second, $\, 50$ for the third, $\, 49$ for the fourth, and $\, 48$ for the fifth. For the number of possible ways to be dealt the first two cards, we compute $52\cdot 51\;$ . For the number of ways to be dealt the first three cards, we have (the number of ways to be dealt the first two cards) $\times$ (the number of ways to be dealt the third card) – here is our new two-step process – or
$(52\cdot 51)\cdot 50 =52\cdot 51\cdot 50$ ways. For the number of ways to be dealt the first four cards, we have (the number of ways to be dealt the first three cards) $\times$ (the number of ways to be dealt the fourth card) – again, a new two-step process – or $(52\cdot 51\cdot 50)\cdot 49 =52\cdot 51\cdot 50\cdot 49$ ways. Finally, the number of ways to be dealt five cards, we have (the number of ways to be dealt the first four cards) $\times$ (the number of ways to be dealt the fifth card) – here again, a two-step process – or $(52\cdot 51\cdot 50\cdot 49)\cdot 48 =52\cdot 51\cdot 50\cdot 49\cdot 48 =311,875,200$ possible outcomes for this process. This would be difficult to count without our technique.
In what follows we will use the above counting technique in a variety of settings, examining its flexibility.
Consider now the number of ways to order a collection of items. Such orderings are called permutations.
Permutations
Here is a model problem. Given a collection of four items, call them $A\,$ , $\, B\,$ , $\, C$ and $D\,$ , in how many ways can we order them? That is, in how many ways can we pick a first item, then a second , then a third, and finally a fourth?
This can be answered by considering it as a multi-step process. There are four ways to pick a first item, then three ways to pick a second, next two ways to pick a third, leaving the fourth item determined (i.e. only one way to pick the fourth item). Thus the number of ways to order the four items is $4\cdot 3\cdot 2\cdot 1 =24\;$ .
In general, the number of ways to order $n$ items is
$$n\cdot (n-1)\cdot (n-2)\cdot \dots \cdot 2\cdot 1 =n!\; \text{.}$$
We see then that the number of ways to shuffle a standard fifty-two card deck is
$$
\begin{array}{rl}
52! & = 80,658,175,170,943,878,571,660,636,856,403,766, \\
& \qquad\qquad 975,289,505,440,883,277,824,000,000,000,000 \\
& \doteq 8.066\times10^{67}\; \text{.}
\end{array}
$$
Having sixty-eight digits, such large numbers readily justify exponential notation!
Still more generally, we might ask for the number of ways to order $k$ of $n$ items (demanding, of course, that $k \le n\,$ ). Such an ordering will be thought of as a $k\,$-step process. There are $n$ possible outcomes for the first step, $\, n-1$ for the second step, and so on until there are $n-k+1$ possible outcomes for the $k\,$-step. Thus the number of possible orderings for $k$ of $n$ items is
$$n\cdot (n-1)\cdot (n-2)\cdot \dots \cdot (n-k+1) =\frac{n!}{(n-k)!}\; \text{.}$$
We will denote this by
$$P_k^n =\frac{n!}{(n-k)!}\, \text{,}$$
although it is worth noting that this notation is by no means universally used.
Thus, for example, the number of ways we can be dealt five cards in order from a standard fair deck is
$$P_5^{52} =\frac{52!}{(52-5)!} =52\cdot 51\cdot 50\cdot 49\cdot 48 =311,875,200\, \text{,}$$
i.e. a bit over three-hundred million.
Another way to think about this
We can think of this as ordering the entire deck, and then considering two orderings the same (for the purposes of being dealt five cards) if the first five cards are in the same order. That is, when being dealt five cards from a shuffled deck, we are only concerned with the order of the first five cards. We receive the same five cards no matter how the final forty-seven cards are ordered. Thus if we group all of the $52!$ possible orderings of the fifty-two card deck into collections for which the first five cards have the same order, each collection has $47! =(52-5)!$ deck orderings in it. Thus the number of collections is
$$ P_5^{52} =\frac{52!}{(52-5)!} \;\text{.} $$
As an application of the above thought process, consider the problem of circular ordering – where $n$ items are placed around a circle with concern only with which is left/right of which, not specific positions on the circle.
Circular Ordering
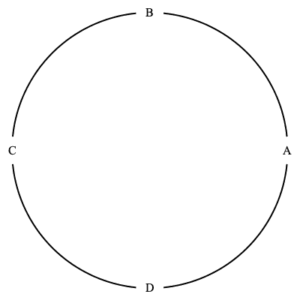
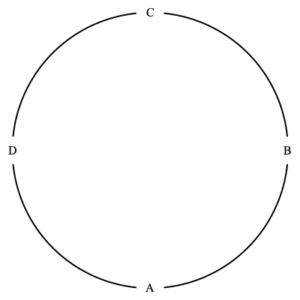
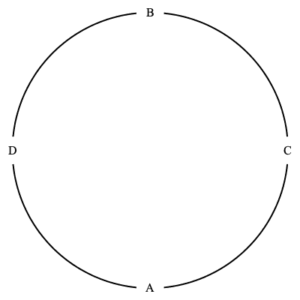
Here we concern ourselves with finding the number of ways to sit $n$ people about a round table, considering two seating arrangements as equal if each person has the same person to their left and to their right. Shown below are two arrangements of four people which are considered identical and a third which is different.
|
|
|
The first two are equivalent seatings, the third is not equivalent to the first two.
The number of such seatings is easily determined by noting that the first person must be somewhere, and any place this person sits is equivalent to any other. Thus we simply put the first person anywhere at the table. The seating of the next $n-1$ people is then a multi-step process, where the first of these people has $n-1$ possible places, the second $n-2\,$ , etc., until all of the $n$ people are seated. This means that there are
$$(n-1)\cdot (n-2)\cdot \dots \cdot 2\cdot 1 =(n-1)!$$
possible seatings.
The discussion is structurally one of circular ordering and the seating of people is used simply to render the process concrete. We have the following.
Fact: There are $(n-1)!$ ways to circularly order $n$ items.
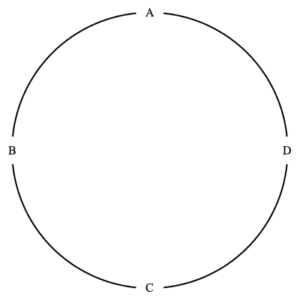
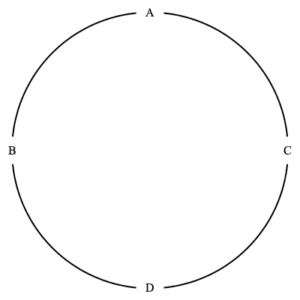
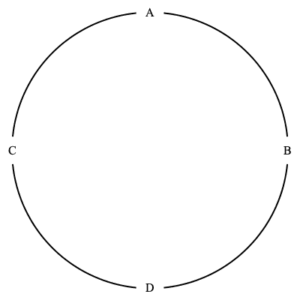
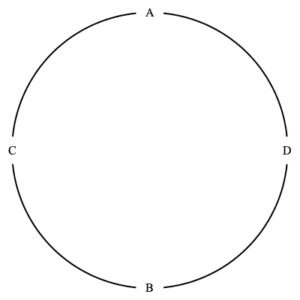
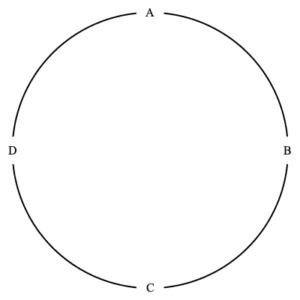
There are thus $(4-1)! =3! =6$ ways to circularly order four items. These are illustrated below. In each we see that item $A$ is at the top of the circle. As noted above, this is just for convenience.
|
|
|
|
|
|
the six different seatings of four people
Another way to think about circular orderings
As in the above discussion of permutations, we have another way to think about the ways to circularly arrange $n$ items. We can consider all $n!$ possible orderings of the $n\,$ , and cluster such orderings into collections as follows. Two orderings are in the same collection if one ordering can be have any tail end relocated to its beginning to obtain the other ordering. Thus if we take the final three items of order $ABCDEFG$ and relocate them to the beginning we get $EFGABCD\;$ . This is the symbolic equivalent to ordering items around a circle and then rotating the circle (as illustrated in the images above). The number of items in each collection is then $n\,$ , so the number of collections is then
$$ \frac{n!}{n} =(n-1)! \;\text{.} $$
This is the number of circular orderings of $n$ items.
Consider for a moment a five-card poker hand. One is dealt five cards and these cards are used to play a hand of poker. The order in which they were dealt is unimportant. We call this a combination of five cards out of the possible fifty-two. What we will be concerned with next is the number of possible combinations of a specific size from a collection of items.
Combinations
$$ P_k^n =\frac{n!}{(n-k)!} \;\text{.} $$
If we wish to consider only the $k$ items, without their ordering, we will consider two such orderings to be equivalent if they are merely re-orderings of each other. Since the number of ways to order $k$ items is $k!\,$ , if we group the ordered collections of $k$ items into clusters where any two are in the same cluster if they are re-orderings of one another, then the number of such clusters is (the number of ways to order $k$ items from a collection of $n\,$ ) divided by (the size of each cluster). That is, the number of
combinations of $k$ items from a collection of $n$ is
$$ \frac{P_k^n}{k!} =\frac{n!}{k!\, (n-k)!} \;\text{.} $$
We denote this by
$$ \left( \begin{array}{c} n \\ k \end{array} \right) =\frac{n!}{k!\, (n-k)!} \, \text{,}$$
and again it is worth noting that this notation is by no means universally used.
Thus, for example, the number of possible poker hands is the number of combinations of five items from a collection of fifty-two, or
$$ \left( \begin{array}{c} 52 \\ 5 \end{array} \right) =\frac{52!}{5!\, 47!} =2598960\; \text{.} $$
We are finally in a position to address the issue raised in the second paragraph of this section: what is the probability of getting a full house on being dealt a five-card poker hand? Assuming as always that we have a fair deck, all hands are equally likely so the probability of getting a full house is precisely the number of full houses divided by the number of possible hands. We have determined the number of poker hands, so we now proceed to determine the number of full houses.
Number of Full Houses as a Case Study in Multi-step Processes
A full house is determined by two card values in order – the card value of the three-of-a-kind and then the card value of the pair, and then determining the suits – and here order is unimportant – of the cards forming the three-of-a-kind and the pair. We now work through this multi-step process.
The number of ways to pick two values in order from thirteen possible values is
$$ P_13^2 =13\cdot 12 =156 \;\text{.} $$
Once we have determined the value of the three-of-a-kind, there are
$$ \left( \begin{array}{c} 4 \\ 3 \end{array} \right) =\frac{4!}{3!\, 1!} =4 $$
ways to pick the suits of the three cards which make up the triple. Next we see that there are
$$ \left( \begin{array}{c} 4 \\ 2 \end{array} \right) =\frac{4!}{2!\, 2!} =6 $$
ways to pick the two cards which make up the pair. Thus there are
$$ 156\cdot 4\cdot 6 =3744 $$
distinct full houses.
The probability of being dealt a full house poker hand is
$$
\frac{\text{number of full houses}}{\text{number of poker hands}} =\frac{3744}{2598960}
=\frac{6}{4165} \doteq .00144 \;\text{.}
$$
This is about one full house in seven hundred fifty poker hands.

